算法篇——冒泡排序与快速排序
冒泡排序
最近清华有个本科生突然火了起来,尤其是最近他的找工作经历,我想让很多同行且在找工作的同学汗颜。很惭愧,我很久就关注这个人了(通过博客),一点点看他如何成为“大神”,而自己却还是平平凡凡。也许平时并没有什么明显很强的感觉,但一找工作实力就体现出来了,料想不久后自己也要找工作,有些着急。。。有时候会想,关注这些大神有什么用,本就对一般人来说不现实。其实道理也很简单,这就像学历史,我们为什么要学历史,绝不仅仅是要学个知识,我们要“以史为鉴”,指导自己的行为。而历史中的人物的智商能力往往强于一般的人(要不也就不会在历史中被记录了,单说正面),我们就是要学习他们的成功之道、处世之道,甚至是失败的原因等等。任何发生过的事情或人(即使是现代),都也成为了历史,我们当然有学习的必要。
题外话就讲到这里,由简到繁先说冒泡排序。冒泡排序算法的思想就是,第一个位置上的元素先和第二个位置上的元素比较,如果大于,则交换两个元素,第一个位置上的元素再和第三个位置上的元素比较,如果大于,再交换位置,依次类推,比较完最后一个元素则第一个位置便是最小的元素。然后第二个位置上的元素再依次比较。重复这一过程直到所有位置上的元素都选定。“冒泡”的名字很形象的表现出这种排序的特点。
void bubbleSort(int arr[], int p, int r)
{
int i, j;
for (i = p; i < r; i++)
for (j = i + 1; j < r; j++)
if (arr[i] > arr[j])
exchange(&arr[j], &arr[i]);
}
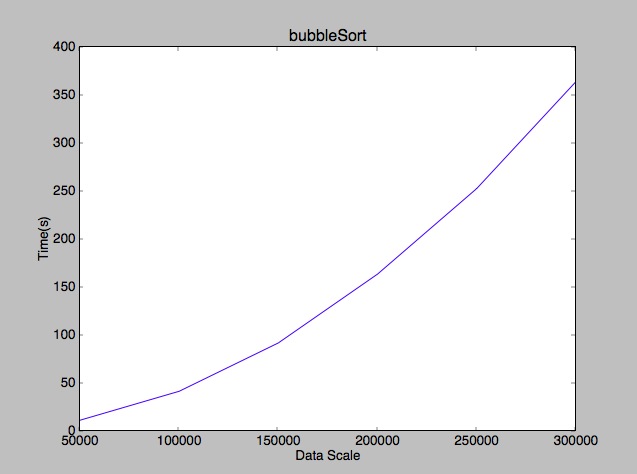
冒泡排序的时间复杂度尽管是n^2,但其排序速度还是非常慢,不像插入排序,冒泡排序每个元素都要与其后所有的元素比较,这无疑让冒泡排序速度非常的慢。
快速排序
快速排序的优点在于其平均复杂度(the average case)比较好,可以达到nlogn,而且具有很小的常数因子。那么这里就会有疑问,一般情况我们都说最差情况下(the worst case)的复杂度,而不是平均情况下的复杂度,这样我们就知道该算法最差能达到多快。的确,最差情况的时间复杂度很重要,但往往情况都是随机的,一般情况显然要远远多于最差的情况,平均复杂度比较好的算法具有很大的优势。其实,很多优秀的算法正是因为其拥有比较好的平均复杂度。
快速排序的主要思想是分而治之,不停的把整个数据按照一定规律分解,进而处理分解后的部分。分解规则是:
| ≤x |=x| >x |将整个数据分解为小于等于x的部分,等于x的部分和大于x的部分。那么这个x如何选择呢,x选择数据中最后一个。算法如下:
int partition(int arr[], int p, int r)
{
int x = arr[r];
int i = p - 1;
int j;
for (j = p; j < r; j++) {
if (arr[j] <= x) {
i++;
exchange(&arr[i], &arr[j]);
}
}
exchange(&arr[i + 1], &arr[r]);
return i + 1;
}
void quickSort(int arr[], int p, int r)
{
int q;
if (p < r) {
q = partition(arr, p, r);
quickSort(arr, p, q - 1);
quickSort(arr, q + 1, r);
}
}
显然这个算法的复杂度由x来决定,如果x比前面的元素都大或小,则数据将被分解为一个没有元素的子数据和一个拥有n-1个元素的子数据。那么复杂度将是:
T(n) = T(n - 1) + T(0) + θ(n)最后得到(画一棵二叉树或使用高中的求数列的方法):
T(n) = θ(n^2)这种情况会出现在已经排好序的数据,而此时使用插入排序,复杂度仅为θ(n)。
那么最好的情况是什么?当然要像归并排序那样正好分为一半。
T(n) = 2T(n/2) + θ(n) = θ(nlogn)如果划分并不是按照1:1划分而是其他划分规则,复杂度是多少?就算是9:1,算法的复杂度依然是θ(nlogn),《算法导论》中有证明,此处不详细叙述。
幸运的话,我们正巧能从中间进行划分,若不幸,则划分为一个拥有n-1的子数据和空数据。如果一系列划分中既有幸运的又有不幸运的(交替分布)会出现什么情况?假设L是幸运的,U是不幸运的。则:
L(n) = 2U(n/2) + θ(n) //lucky
U(n) = L(n - 1) + θ(n) //unlucky经过整理:
L(n) = 2(L(n/2 - 1) + θ(n/2)) + θ(n/2)
= 2L(n/2 - 1) + θ(n)
= θ(nlogn)就是说,好与差交替分布时,快速排序的运行时间如全是好的情况是一样的,那么如何保证这种情况?
当随机选取x时,我们可以使时间复杂度控制在nlogn。代码如下:
int randomPartition(int arr[], int p, int r)
{
int i = p + rand() % (r - p + 1);
exchange(&arr[r], &arr[i]);
return partition(arr, p, r);
}
void quickSort(int arr[], int p, int r)
{
int q;
if (p < r) {
q = randomPartition(arr, p, r);
quickSort(arr, p, q - 1);
quickSort(arr, q + 1, r);
}
}
partition与上面代码相同。我们可以发现每次划分前选择的x是p到r之间的某个随机数,而不是数据的最后一个元素。为什么这种处理就会使平均复杂度为nlogn?
下面的证明方法来自《算法导论》的教学视频,这门公开课视频中有很多比书中更简单或更容易理解的方法。记得以前有个数学老师曾经说过,最好的方法就是“用字母表示事件”,设置随机变量来解决问题,好吧,学好概率论和数理统计真的很重要。
假设随机变量Xk = 1,如果数据可以被划分为k至n-k+1,否则为0。

则Xk的期望为:
![]()
设时间复杂度为T(n):
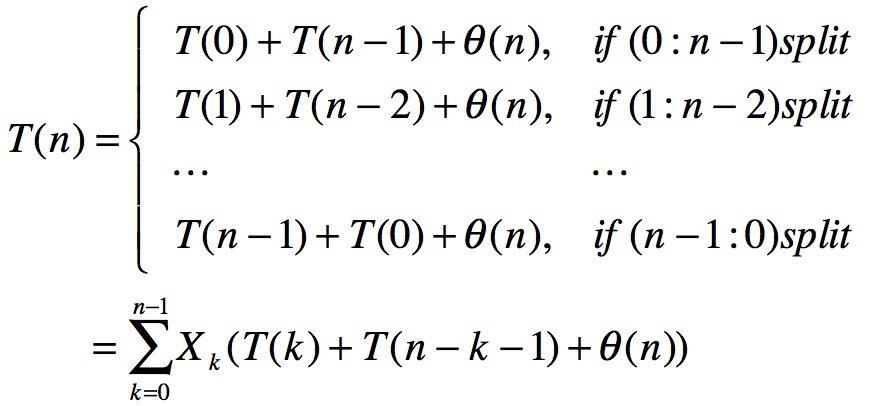
接下来求解T(n)的期望值:
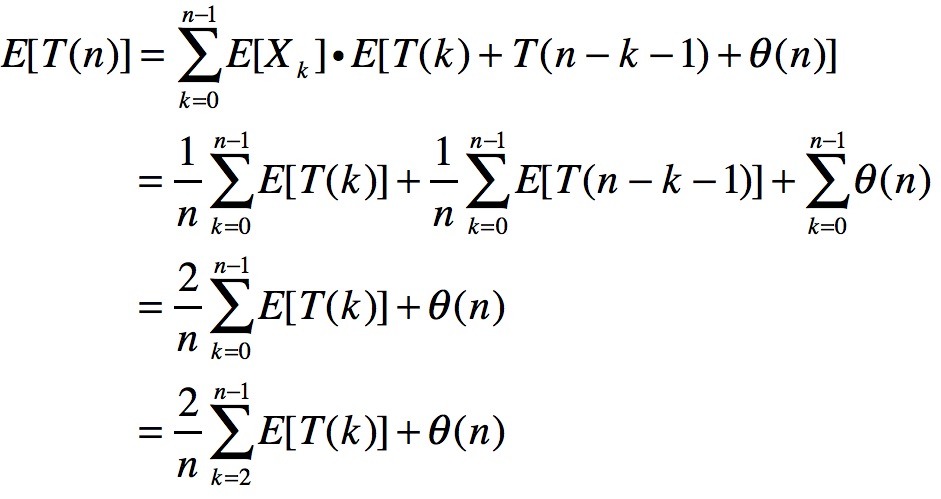
看到倒数第二行,将k扩大至2开始,其效果相当于增大θ(n)。这么做的原因是,想把期望值往logn上靠,如果n是0或1则在处理上会有难度,此处的处理避开了0和1的log算术。
接下来要用到一个公式:
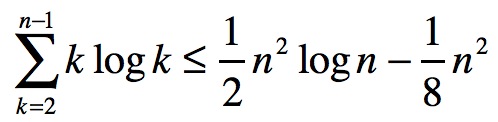
借此再次处理期望值:
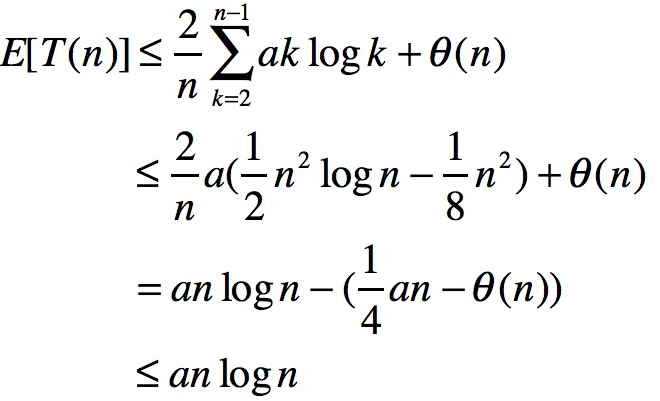
那第一步为什么会小于或等于含有aklogk,这是因为二叉树的原因,书中有所讲解。我们发现如果a很大时,使an/4大于θ(n),E[T(n)]是小于或等于anlogn的。
到这里,我们可以看到快速排序的平均复杂度是趋近与nlogn的(打这些公式好累啊。。。),最好上个性能图:
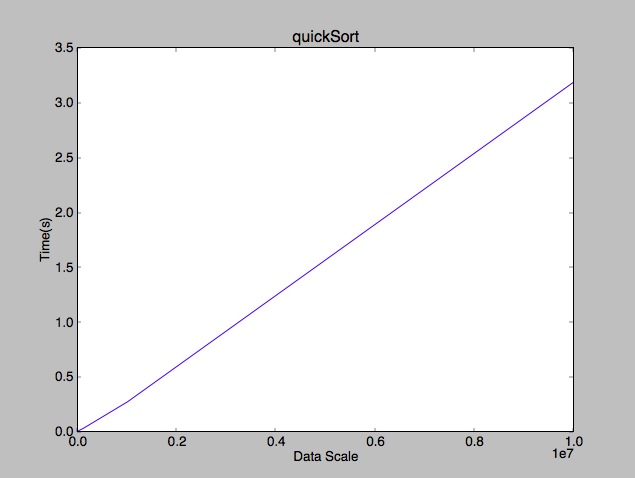
blog comments powered by Disqus